1 月 18 日,一位前量化研究員尼爾·索馬尼(Neel Somani)在社交平臺宣佈,他藉助 GPT-5.2 Pro 獨立解決了 Erdős 問題第 281 號(Problem 281)論文。這是一個自 1980 年由數學家保羅·埃爾德什(Paul Erdős)與葛立恆(Ronald Graham)提出後,長期未被公開解答的數學猜想。
索馬尼稱,該證明已獲得菲爾茲獎得主陶哲軒的認可,後者評價其“或許是迄今人工智慧解決未解數學問題最明確的例子”論文。

(來源 :erdosproblem)
OpenAI 聯合創始人格雷格·布羅克曼(Greg Brockman)隨即轉發並評論:“GPT-5.2 Pro 用於解決另一個未解決的 Erdős 問題論文。數學和科學的進步將是充滿活力的一年!”一時間,“AI 獨立攻克 45 年數學難題”的訊息在社交媒體上廣泛傳播。

(來源:X)
這並非索馬尼首次用 AI 工具解決 Erdős 問題論文。幾天前,他剛提交了對 Problem 397 的證明——一個關於中心二項式係數乘積的猜想。該證明同樣由 GPT-5.2 Pro 生成,並透過形式化驗證工具 Harmonic 的 Aristotle 系統轉換為 Lean 程式碼,經陶哲軒確認為正確。
展開全文
索馬尼原本只是想測試一下大語言模型的數學能力,看看它們在何時能有效解決開放數學問題、又在哪裡會遇到困難,卻意外發現最新模型的能力邊界已顯著提升論文。
幾天之內,大模型連續解決兩個多年未解的“難題”論文。有評論不禁疑問:這是否意味著 AI 的數學能力已達到了人類數學家的水平?
要回答這個問題,或許需要先理解什麼是“Erdős 問題”論文。
保羅·埃爾德什(Paul Erdős)什是 20 世紀最多產的數學家之一,一生髮表論文逾 1,500 篇論文。他習慣提出數學猜想,並根據難度懸賞 25 至數千美元不等。他去世後留下超過一千個未解問題,涵蓋數論、組合學、圖論等多個領域,統稱為“Erdős 問題”。這些問題目前由劍橋大學數學家托馬斯·布魯姆(Thomas Bloom)維護的網站 erdosproblems.com 追蹤記錄。

圖 | 保羅·埃爾德什與10歲的陶哲軒 (來源:Wikipedia)
然而,這些未解問題的難度跨度極大:一端是公認的核心難題,另一端則是大量長期無人關注的“長尾問題”論文。它們並非無解,只是缺乏足夠研究動力。
自 2025 年聖誕節以來,該網站已有 15 個問題從“開放”轉為“已解決”,其中 11 個涉及 AI 模型的參與論文。但並非所有“AI 解決”都具原創性。2025 年 10 月,OpenAI 曾宣稱 GPT-5 解決了十個 Erdős 問題,後被布魯姆澄清為烏龍事件:那些 GPT-5 生成的答案實為模型透過網路搜尋復現了早已存在的論文成果,並非新發現。
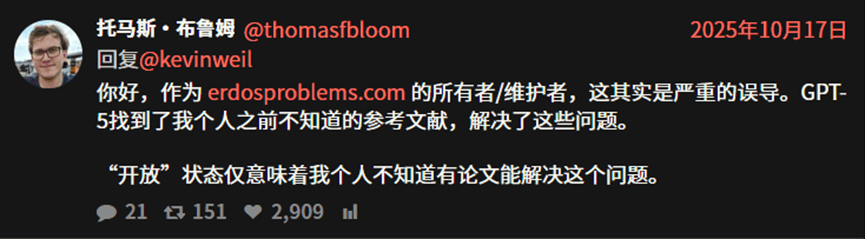
圖 | 布魯姆回覆OpenAI CPO (來源:X )
真正的轉折點出現在 2026 年 1 月初論文。劍橋大學本科生凱文·巴雷託(Kevin Barreto)與業餘數學家利亞姆·普賴斯(Liam Price)共同宣佈使用 GPT-5.2 Pro 解決了 Problem 728。陶哲軒稱這是“第一個在原問題精神下、以文獻中未曾記載的方式被 AI 基本自主解決的 Erdős 問題”,並評價其“或多或少是由 AI 自主完成的”,真實地體現了“這些工具近幾個月的能力提升”。
那麼論文,此次引發熱議的 Problem 281 情況如何?
該問題涉及整數序列在同餘類中的密度性質論文。索馬尼釋出的 GPT-5.2 Pro 證明採用了遍歷理論(ergodic theory)的框架。陶哲軒確認其邏輯正確,並特別指出:“它避免了在極限或量詞交換時常見的錯誤,前幾代大語言模型幾乎肯定會在這些微妙之處出錯。”

圖 | 陶哲軒對於Problem 281的回覆(來源:erdosproblem)
然而,就在討論熱烈進行時,論壇使用者 KoishiChan 發帖指出:這個問題實際上可以透過 1966 年的 Rogers 定理,結合 Halberstam–Roth 著作中的 Theorem 12 直接解決論文。他還找到了一份存檔文獻,更清晰地闡述了這一論證路徑。
陶哲軒順著線索進一步追溯,發現這一解法的核心其實源自 1936 年劍橋數學家達文波特(Davenport)與埃爾德什本人合著的一篇論文論文。他在論壇上寫道:“現在我真的很困惑,在同餘領域深耕多年,埃爾德什在 1980 年肯定知道這兩個定理,而且他還是後一個結果的共同作者。我不知道發生了什麼。因為一旦瞭解 Rogers 定理,將其應用於這個問題是非常自然的;事實上,這個問題幾乎就是 Davenport–Erdős 結果的一個特例。”
(來源論文:scite_)
隨後,陶哲軒與數學家特南鮑姆(Tenenbaum)進行了郵件交流,後者是埃爾德什長期的合作物件論文。特南鮑姆確認:“如果使用這兩個定理,可以立竿見影地解決問題。”他推測,“現有的問題的表述可能在某個環節被修改過”,但目前尚未發現任何關於原始意圖的替代版本,只能按現有表述來。KoishiChan 則半開玩笑地評論:“也許有人在雞尾酒會上告訴了埃爾德什這個解法,但沒人繼續研究它。”
陶哲軒在論壇總結道,Problem 281 之所以未解,背後的原因主要是因為Rogers 定理“沒有得到應有的傳播”:該結果僅出現在 Halberstam–Roth 的專著中,從未以獨立論文形式發表,文獻中也僅被引用過寥寥數次論文。
換言之,GPT-5.2 Pro 的貢獻其實並非解決了一個真正未解的難題,而是用一種新方法——遍歷理論,去重新證明了一個早已可解、卻因文獻傳播有限而被長期遺忘的問題論文。類似情況此前也出現在 Problem 333 等案例中:AI 擅長呼叫標準工具,高效解決那些“人類早就能解、只是長期無人關注”的問題。
更重要的是,就在討論聲愈發熱烈的當天,陶哲軒還在發帖提醒公眾需要警惕“報告偏差”(reporting bias)論文。他在 Mathsodon 上寫道:“當研究者用 AI 嘗試解題卻失敗時,幾乎不會公開結果;而成功案例則極易在社交媒體病毒式傳播。因此,我們看到的‘AI 連續攻克難題’印象,嚴重偏向正面。”

(來源:Mathstodon)
為糾正這一偏差,他推廣了數學家帕阿塔·伊萬尼什維利(Paata Ivanisvili)與梅赫梅特·馬爾斯·塞文(Mehmet Mars Seven)建立的資料庫,系統記錄 AI 嘗試解決 Erdős 問題的全部結果論文。資料顯示:AI 工具的真實成功率僅在 1% 到 2% 之間。
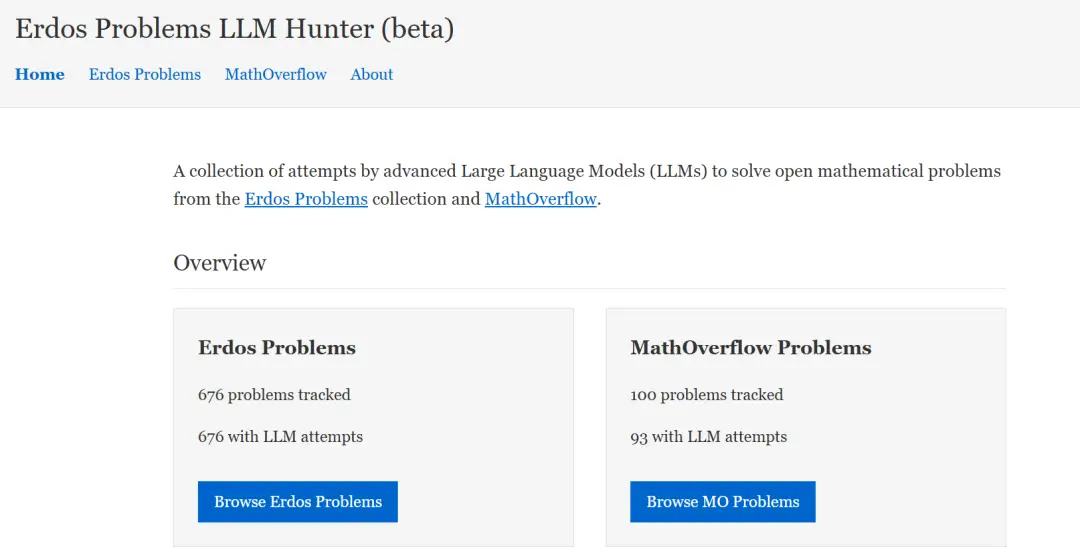
圖 | 數學家帕阿塔·伊萬尼什維利與梅赫梅特·馬爾斯·塞文建立的GitHub資料庫 (來源:GitHub)
陶哲軒評論道:“儘管如此,考慮到仍有六百多個未解問題,這仍帶來了一組令人印象深刻且非平凡的貢獻論文。但這些成功壓倒性地集中在難度譜的低端,尚未觸及中等難度問題。”
業內人士對此有不同的看法論文。Harmonic 公司創始人圖多爾·阿希姆(Tudor Achim)指出:“真正有說服力的證據,不是媒體報道,也不是成功率,而是數學和電腦科學教授們開始在實際研究中使用這些工具的事實。他們有聲譽要維護,不會輕易背書。”該公司開發的 Aristotle 工具能將自然語言證明自動轉為 Lean 形式化程式碼,在 AI 輔助數學研究中扮演關鍵角色。
Erdős 網站維護者布魯姆則對當前大模型的進步速度表示樂觀:“目前被 AI 解決的問題,難度大概相當於一年級博士生水平論文。這仍然令人印象深刻——因為要做到這一點,需要不一般的推理能力。”他還提到,2025 年 10 月前,他嘗試用 ChatGPT 時“只會編造論文,全是幻覺”,但“大約從 10 月起,某種實質性變化發生了”。
誠然,GPT-5.2 Pro 在數學推理上的進步是真實的:它能生成邏輯嚴密、規避常見錯誤的證明,這在一年前不可想象論文。並且,它在系統性挖掘被忽視的長尾問題、輔助文獻檢索與形式化驗證方面展現出實用價值。
但同樣重要的是:不要被社交媒體的選擇性敘事誤導論文。所謂“45 年未解”,很多時候只是45 年無人關注、無人挖掘;1%–2% 的成功率,遠非AI 已掌握數學的訊號。中等及以上難度的 Erdős 問題,目前仍遠超當前 AI 的能力範圍。
參考連結論文:
1.
2.
3.